布隆过滤器是一种以牺牲一部分正确率来换取空间复杂度的数据结构，其中误报指的是可能会判断不存在的元素为可能存在，但在判断不存在的元素时不会出现误报，即返回为True时元素可能存在，返回False时元素一定不存在。下表是布隆过滤器的误报率，m为元素总个数，n为过滤器长度，k为hash函数的个数。

m/n	k	k=1	k=2	k=3	k=4	k=5	k=6
2	1.39	0.393	0.400
3	2.08	0.283	0.237	0.253
4	2.77	0.221	0.155	0.147	0.160
5	3.46	0.181	0.109	0.092	0.092	0.101
6	4.16	0.154	0.0804	0.0609	0.0561	0.0578	0.0638
7	4.85	0.133	0.0618	0.0423	0.0359	0.0347	0.0364

由表中数据可以得出误报率最小时k≈0.7m/n

import mmh3
from bitarray import bitarray


class BloomFilter:
    def __init__(self, size, hash_count):
        self._bit_size = size
        self._bit = bitarray(self._bit_size)
        self._hash_count = hash_count

    def _get_hash_index(self, data):
        return [mmh3.hash(str(data), i) % self._bit_size for i in range(self._hash_count)]

    def add(self, data):
        index_list = self._get_hash_index(data)
        for index in index_list:
            self._bit[index] = 1

    def is_contains(self, data):
        index_list = self._get_hash_index(data)
        for index in index_list:
            if self._bit[index] == 0:
                return False
        return True

原理

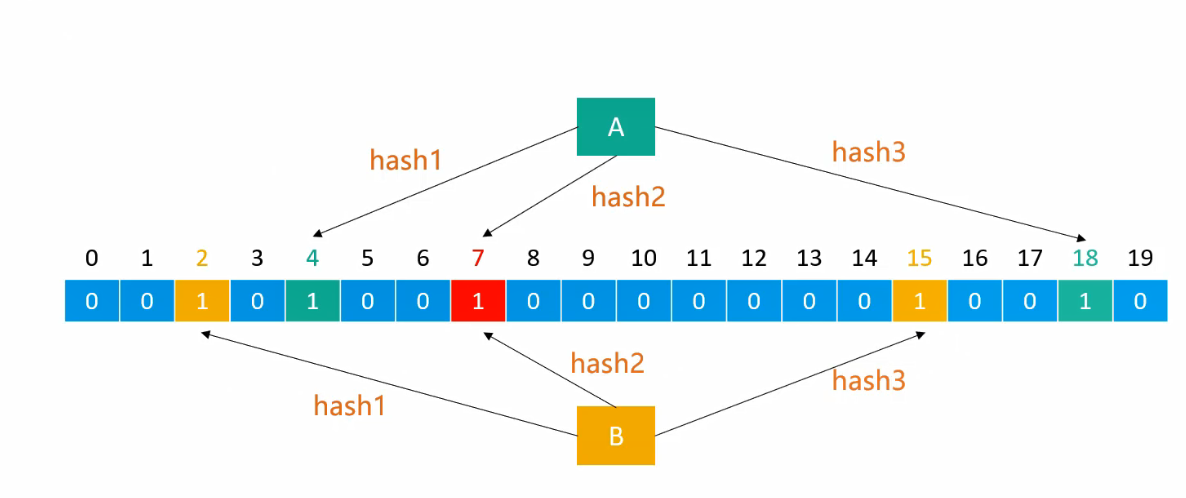
布隆过滤器中，二进制数组的长度和哈希函数的个数由问题的数量规模、要求的错误率决定。假设图示中大小为20的二进制数组与3个哈希函数满足了问题需求，那么向布隆过滤器添加元素时，将每一个哈希函数生成的索引位置都设为 1。查询元素是否存在时，如果有一个哈希函数生成的索引位置不为 1，就代表不存在（100%准确）；如果每一个哈希函数生成的索引位置都为 1，就代表存在（存在一定的误判率）。 Description

布隆过滤器添加、查询的时间复杂度都是：O(k) ，k 是哈希函数的个数。空间复杂度是：O(m) ，m 是二进制位的个数。

数值计算

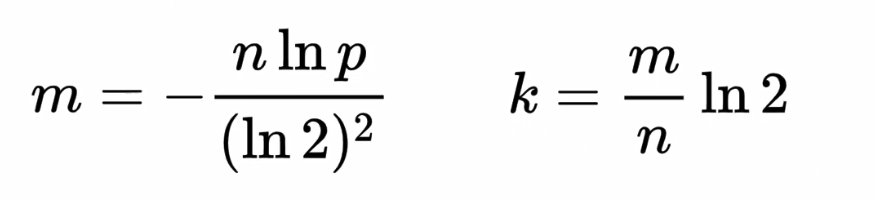
已知误判率 p、数据规模 n，求二进制位的个数 m、哈希函数的个数 k，较为合理的计算公式如下，公式由科学家给出。 Description

Python代码实现

'''
布隆过滤器，在大量的数据中，判断某个数据是否存在时经常使用，有非常高效的空间效率与查询效率
缺点：存在一定的误判率
n:数据规模 p:要求的误判率
二进制数据位数 m=-n*lnp/(ln2)^2
哈希函数个数 k=m/n*ln2
'''
import ctypes
import math

class BloomFilter():
    def __init__(self,n:int,p:float):
        '''
        :param n:数据规模
        :param p:误判率
        '''
        #计算二进制数组规模与hash函数数量
        self.bitSize=int(-n*math.log(p)/math.pow(math.log(2),2))
        self.hashFuncSize=int(self.bitSize*math.log(2)/n)
        self.bitArray=[0]*(int((self.bitSize+32-1)/32))

    def put(self,value):
        '''
        :param value:存入的数据
        '''
        self.valueCheck(value)
        #哈希值的设置参考google布隆过滤器源码
        hash1=value.__hash__()
        hash2=self.unsigned_right_shitf(hash1,16)
        for i in range(self.hashFuncSize):
            combinedHash=hash1+i*hash2
            if combinedHash<0:
                combinedHash=~combinedHash
            combinedHash=combinedHash%self.bitSize
            index=int(combinedHash/32)#位于第index个int元素
            position=combinedHash-index*32#在int中的位置
            self.bitArray[index]=self.bitArray[index]|(1<<position)

    def contains(self,value):
        '''
        :param value:判断是否存在的数据
        :return:True or False
        '''
        self.valueCheck(value)
        hash1 = value.__hash__()
        hash2 = self.unsigned_right_shitf(hash1,16)
        for i in range(self.hashFuncSize):
            combinedHash = hash1 + i * hash2
            if combinedHash < 0:
                combinedHash = ~combinedHash
            combinedHash = combinedHash % self.bitSize
            index = int(combinedHash / 32)  # 位于第index个int元素
            position = combinedHash - index * 32  # 在int中的位置
            result= self.bitArray[index] & (1 << position)
            if result==0:
                return False
        return True

    def valueCheck(self, value):
        if value != 0 and not value:
            print('value can\'t be None')

    def int_overflow(self,val):
        maxint = 2147483647
        if not -maxint - 1 <= val <= maxint:
            val = (val + (maxint + 1)) % (2 * (maxint + 1)) - maxint - 1
        return val

    #无符号右移
    def unsigned_right_shitf(self,n, i):
        # 数字小于0，则转为32位无符号uint
        if n < 0:
            n = ctypes.c_uint32(n).value
        # 正常位移位数是为正数，但是为了兼容js之类的，负数就右移变成左移好了
        if i < 0:
            return -self.int_overflow(n << abs(i))
        # print(n)
        return self.int_overflow(n >> i)


if __name__=='__main__':
    n=100000000
    p=0.01
    bf=BloomFilter(n,p)
    total_size=100000
    error_count=0
    for i in range(total_size):
        bf.put(i)
    for i in range(total_size):
        if not bf.contains(i):
            error_count+=1
    print('error rate :',float(error_count/total_size) if error_count>0 else 0)

版权声明：如无特殊说明，文章均为本站原创，转载请注明出处

本文链接：http://kkxl95.cn/article/1658907633562/